by Joachim Schubart, Astron.Rechen-Institut, Heidelberg, Germany
The present Part 2 is a continuation of the earlier file
News on HILDA ASTEROIDS, here called Part 1.
Since the introduction of Part 1 gives the necessary explanations and formulas,
the introduction of Part 2 can be brief.
Epm, Ip, and Ampl.Remarks on Section 2 inserted in May 2007: Due to the simple model of the forces and to other simplifications, the following results are not final, but qualitatively correct in case of (1578) Kirkwood and in other cases. However, the indicated evolution of the orbit of (38553) is not confirmed by a more accurate model of the forces. A more rigorous treatment of the subject appears in J.Schubart's paper "Additional Effects of Resonance in Hilda-Asteroid Orbits by the combined Action of Jupiter and Saturn", Icarus 188, pp. 189-194, May 2007. In the following text the frequency n represents a mean value of the mean motion of the asteroid with respect to the period of libration of crarg'.
Some of the values of Ampl listed in the Appendix of Part 1 appear at lower accuracy, since results from a basic interval of integration of about 23000 yr and from 1/3 or 1/2 of this interval differ by 2 or 3 deg in such unusual cases. Almost all of these cases correspond to values of Ampl near 60 deg. (499) Venusia and (1578) Kirkwood represent such cases. Now the study of their orbits and of some other cases has led to the discovery of another type of resonance in the resonance. Contrary to the well-known secondary resonances that involve the period of libration of crarg' and the long periods arising from the motion of perihelion and node, now a linear combination of the orbital frequencies of asteroid and perturbing planets is commensurable to the frequency of the period of libration.
The study started with an extension of the basic numerical integration on (499) and (1578) to an interval of about 120 000 yr centered at the present time. As before, sun, Jupiter, Saturn, and the two asteroids are the attracting or moving bodies in a simultaneous integration. Sets of elements, stored at evenly spaced intervals, allow the derivation of crarg' of an asteroid as a function of time. Digital filtering isolates the effects by the period of libration, and a plot versus time shows the resulting oscillation of crarg' and the interesting changes of amplitude in each case. The circulation of lp - lpj, the difference of the longitudes of perihelion of asteroid and Jupiter, causes a comparatively small effect in amplitude, but long-period changes in amplitude between about 56 and 63 deg are irregular and follow variable periods between 20000 to 40000 yr about in both cases. These long-period effects disappear, if the attraction of Saturn is neglected.
After a break, the study has continued in early 2005. Considering the possibility that a resonance acts on asteroids with Ampl near 60 deg, I have isolated by digital filtering the frequencies that rule the variations of the semi-major axis of (1578) in the simplified model of the restricted three-body problem. ncr, the frequency of the period of libration of crarg', n-nj, the difference of the mean motions of asteroid and Jupiter that corresponds to the relative circulation in longitude, and linear combinations of these two frequencies have appeared in this way. When I changed these values of frequency to the respective periods, almost instantly I realized that a period of about 20 yr derived from n - nj + 2 ncr nearly equals the period of the relative revolution of Jupiter with respect to the direction sun - Saturn. The frequency of this period is given by nj-ns, the difference of the mean motions of Jupiter and Saturn. Returning to the original sun - Jupiter - Saturn integration, I was able to confirm the approximate relation nj - ns = n - nj +2 ncr in higher accuracy. This means:
2 ncr = (nj-ns) - (n-nj)
phi = 2 lmj - lm - lms .

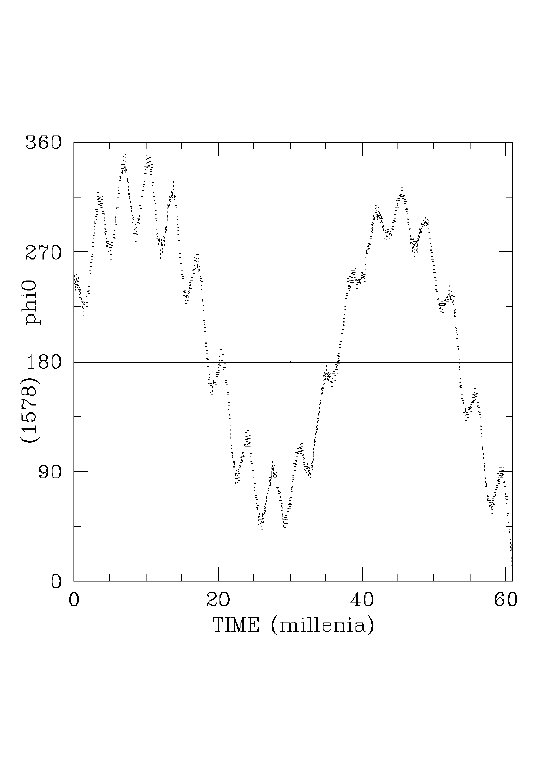
Fig.1 has resulted from the forward computation on (1578) and shows a long-period libration of phi0 about 180 deg with variable amplitude, together with effects by the period of circulation of lp-lpj. The libration turns out to be temporary, since according to the backward integration of (1578) phi0 can cross the unstable level of 0 or 360 deg and show circulation. In case of (499) the forward integration shows one half of a cycle of libration that is followed by circulation of phi0, but only libration of phi0 about 180 deg results from the backward computation. An influence of the long-lasting secular increase or decrease of the eccentricity of Jupiter on the amplitude of the observed libration of phi0, or on the changes between libration and circulation, is indicated. However, the variations of phi0 and the observed effects in the amplitude of crarg' are clearly correlated in all studied cases: Neglect the superimposed oscillations as shown in Fig.1 and compare the long-period variations of phi0 with the observed long-period effects in the amplitude of crarg'. If phi0 passes the level of 180 deg in the downward or upward direction, a maximum or minimum of these effects in the amplitude of crarg' occurs, respectively. Less important extremes occur, if phi0 crosses the 0 or 360 deg level during circulation. According to this, the observed long-period variations in the amplitude of crarg' are an effect of the considered resonance.
A non-quasiperiodic evolution is evident in case of orbits with changes between libration and circulation of phi0. In spite of this, a rough guess about a proper parameter Ampl for such cases is worth an attempt. I assume that plots as mentioned above show the long-period variations of the amplitude of crarg' versus time. For Ampl of such an orbit, I shall use a round mean value of the maximum and minimum of these variations shown in a plot that corresponds to an interval with libration of phi0, although intervals with circulation of phi0 in either the upward or the downward direction will show different mean values. Much more extended integrations are necessary to find out whether such a guess is meaningful. For (499) and (1578) I shall use Ampl = 60 deg.
I have examined some other Hildas with numbers less than 40000 for effects
by the additional resonance. (21804) Vaclavneumann again shows changes between
libration and circulation of phi0. Since it is a case of analogy to (499), I
use Ampl = 60 deg. Two other objects, (23405) Nisyros and (39382) Opportunity,
perform about one and a half cycle of libration of phi0 about 180 deg during
the interval of 60000 yr of a forward integration. The amplitudes are similar
to the ones shown in the central part of Fig.1, but there is no indication of
large changes of these amplitudes. I propose 63 for Ampl of (23405) and 60 for
(39382). Comparing these and the preceding values of Ampl with the respective
round values in the Appendix of Part 1, I find no difference of more than one
degree.
I have found more Hildas with a strong relation to the additional
resonance: (37578) and (38553). According to a forward integration covering
48000 yr, phi0 of these asteroids passes the 180 deg level after about 10000 yr,
but later on the mean variations of phi0 of both objects become very slow in
a gradual approach to the unstable level of 0 or 360 deg.
After this approach, that lasts about 10000 yr, phi0 of (37578) shows libration
by a return to 180 deg, but phi0 of (38553) has crossed the 360 deg level,
showing circulation. I use Ampl = 61 for (37578) and propose 60 for (38553),
since I assume that this object can show temporary libration of phi0 as well.
For these two cases the procedure of Part 1 did not signal an uncertainty in
the determination of Ampl, and the values proposed here differ by about 2.5 deg
from those of Part 1.
I have studied (1202) Marina by a forward integration over 48000 yr, since it is a representative of Hildas in the vicinity of the additional resonance, but not in the central domain with temporary libration of phi0. In this case phi0 circulates and passes the 180 deg level every 15000 yr in the downward direction. A small effect in the amplitude of crarg' corresponds to this comparatively fast circulation. The procedure of Part 1 appears as suitable for such cases, the value Ampl = 65 deg of (1202) is confirmed by the more extended integration. However, a value of Ampl given in Part 1 is possibly uncertain, if a Hilda resembles (499) or (23405), for instance, in all the values of Epm, Ampl, and TL. The next section presents these values for many objects with numbers less than 40000.
No. Asteroid Epm k Ampl TL
deg yr
1 ( 153) 0.1719 1.36 18.7 270.3
2 ( 190) 0.1693 1.38 40.4 261.6
3 ( 361) 0.2044 1.48 46.1 265.6
4 ( 499) 0.200 1.44 60 248
5 ( 748) 0.1682 1.36 43.9 258.4
6 ( 958) 0.1711 1.38 47.5 259.3
7 ( 1038) 0.1618 1.42 56.8 258.9
8 ( 1162) 0.1401 1.34 50.7 256.6
9 ( 1180) 0.1665 1.35 39.3 262.6
10 ( 1202) 0.1243 1.31 65.0 252.5
11 ( 1212) 0.2300 1.47 25.3 263.6
12 ( 1268) 0.1334 1.32 48.5 260.4
13 ( 1269) 0.1245 1.32 88.8 238.5
14 ( 1345) 0.2022 1.44 28.9 269.1
15 ( 1439) 0.1749 1.39 48.4 256.4
16 ( 1512) 0.1933 1.41 47.1 258.4
17 ( 1529) 0.1518 1.37 67.1 254.2
18 ( 1578) 0.202 1.44 60 248
19 ( 1746) 0.1388 1.32 23.5 272.6
20 ( 1748) 0.1767 1.39 64.3 247.5
21 ( 1754) 0.1912 1.44 48.8 264.6
22 ( 1877) 0.2039 1.44 36.6 279.3
23 ( 1902) 0.1882 1.40 11.8 273.9
24 ( 1911) 0.1894 1.39 26.9 262.3
25 ( 1941) 0.2162 1.45 49.6 253.4
26 ( 2067) 0.1750 1.38 33.6 261.1
27 ( 2246) 0.1506 1.34 37.2 264.0
28 ( 2312) 0.1099 1.30 36.6 265.0
29 ( 2483) 0.2463 1.55 23.0 262.1
30 ( 2624) 0.1098 1.28 31.3 264.5
31 ( 2760) 0.1771 1.37 51.5 270.1
32 ( 2959) 0.2121 1.47 41.1 257.7
33 ( 3134) 0.1821 1.42 33.4 266.6
34 ( 3202) 0.1263 1.35 61.4 268.5
35 ( 3254) 0.1103 1.30 43.0 262.8
36 ( 3290) 0.1956 1.40 31.6 260.6
37 ( 3415) 0.1856 1.37 5.0 265.5
38 ( 3514) 0.1255 1.34 52.0 258.5
39 ( 3557) 0.1724 1.37 61.0 252.6
40 ( 3561) 0.1302 1.32 18.4 272.9
41 ( 3571) 0.1249 1.31 44.4 269.3
42 ( 3577) 0.1929 1.43 48.9 256.2
43 ( 3655) 0.1553 1.37 75.8 244.2
44 ( 3694) 0.1317 1.32 58.9 258.0
45 ( 3843) 0.1159 1.30 72.1 251.3
46 ( 3923) 0.1949 1.40 22.8 263.0
47 ( 3990) 0.1667 1.37 36.1 268.0
48 ( 4230) 0.1956 1.39 23.7 263.0
49 ( 4255) 0.1961 1.40 25.7 262.5
50 ( 4317) 0.2128 1.46 38.3 263.2
51 ( 4446) 0.2703 1.60 29.3 259.8
52 ( 4495) 0.1228 1.35 89.8 244.0
53 ( 4757) 0.1363 1.30 27.2 263.7
54 ( 5368) 0.1310 1.31 28.8 267.3
55 ( 5439) 0.1234 1.33 74.6 247.3
56 ( 5603) 0.1292 1.31 58.7 256.5
57 ( 5661) 0.1960 1.44 39.2 273.1
58 ( 5711) 0.1392 1.33 32.9 266.3
59 ( 5928) 0.1586 1.36 19.0 271.1
60 ( 6124) 0.1904 1.43 35.0 265.2
61 ( 6237) 0.1108 1.29 58.6 259.7
62 ( 6984) 0.1992 1.44 22.7 280.7
63 ( 7027) 0.1873 1.41 34.0 269.8
64 ( 7174) 0.2047 1.43 50.1 265.4
65 ( 7284) 0.1657 1.36 55.3 255.5
66 ( 8086) 0.1797 1.38 37.8 269.4
67 ( 8130) 0.2142 1.45 50.3 253.9
68 ( 8376) 0.1884 1.40 38.7 259.0
69 ( 8550) 0.1887 1.40 30.9 261.6
70 ( 8551) 0.1484 1.36 42.5 275.5
71 ( 8743) 0.1702 1.38 48.9 275.9
72 ( 8913) 0.1962 1.39 26.3 262.4
73 ( 8915) 0.0969 1.28 38.1 265.5
74 ( 9661) 0.1743 1.40 39.8 270.1
75 ( 9829) 0.1906 1.39 23.9 262.9
76 (10063) 0.1119 1.29 45.7 260.3
77 (10296) 0.2199 1.46 47.5 253.9
78 (10331) 0.1837 1.39 40.5 258.9
79 (10608) 0.2167 1.44 46.5 255.0
80 (10610) 0.1524 1.33 20.9 265.5
81 (10632) 0.1364 1.36 60.3 258.6
82 (11175) 0.1372 1.33 9.4
83 (11249) 0.1907 1.43 34.8 274.3
84 (11274) 0.1749 1.38 73.4 241.7
85 (11388) 0.1550 1.36 55.6 260.7
86 (11410) 0.1455 1.35 36.9 263.6
87 (11542) 0.2003 1.43 44.4 258.9
88 (11739) 0.1758 1.48 57.1 266.3
89 (11951) 0.1575 1.35 41.9 260.1
90 (12006) 0.1400 1.37 60.9 265.6
91 (12307) 0.1919 1.40 29.4 261.7
92 (12896) 0.2163 1.47 41.7 258.5
93 (12920) 0.1942 1.43 49.5 257.7
94 (13035) 0.1942 1.39 23.5 263.3
95 (13317) 0.1514 1.33 28.0 267.0
96 (13381) 0.1953 1.40 32.6 262.0
97 (13504) 0.2165 1.50 40.7 273.6
98 (13897) 0.1355 1.36 65.2 259.2
99 (14195) 0.1866 1.40 29.0 267.3
100 (14569) 0.2188 1.48 39.9 265.3
101 (14669) 0.1339 1.32 43.1 263.4
102 (14845) 0.1918 1.40 20.3 265.1
103 (15068) 0.2068 1.44 50.0 253.1
104 (15231) 0.2136 1.45 38.9 260.2
105 (15278) 0.1746 1.41 56.6 259.9
106 (15373) 0.1196 1.30 8.3
(15376) see below
107 (15426) 0.1057 1.31 54.6 263.2
108 (15505) 0.1774 1.40 62.2 254.7
109 (15540) 0.1875 1.40 34.9 278.5
110 (15545) 0.1950 1.39 27.0 262.2
111 (15615) 0.1971 1.39 23.3 263.0
112 (15638) 0.1434 1.34 48.3 264.5
113 (15671) 0.1683 1.40 65.9 252.0
114 (15783) 0.2014 1.42 48.9 256.2
115 (16232) 0.1626 1.37 35.0 267.5
116 (16843) 0.1794 1.37 31.6 263.0
117 (16915) 0.1925 1.41 45.9 260.7
118 (16927) 0.1448 1.35 49.9 273.4
119 (16970) 0.1380 1.34 28.7 272.6
120 (17212) 0.2043 1.43 23.5 267.4
121 (17305) 0.1710 1.41 64.0 252.6
122 (17428) 0.1657 1.37 44.9 265.4
123 (17867) 0.1357 1.31 29.6 268.1
124 (18036) 0.1961 1.40 25.7 262.6
125 (19034) 0.1922 1.39 25.5 262.6
(19752) see below
126 (20038) 0.1993 1.46 31.8 284.3
127 (20628) 0.1928 1.45 59.7 251.3
128 (20630) 0.2302 1.49 45.4 253.8
129 (20640) 0.1667 1.36 11.4 269.8
130 (21047) 0.1358 1.31 39.1 262.2
131 (21128) 0.1696 1.39 58.0 258.5
132 (21804) 0.193 1.42 60 249
133 (21930) 0.1823 1.37 28.5 262.3
134 (22058) 0.1611 1.41 70.2 249.3
135 (22070) 0.2168 1.48 16.0 273.8
136 (22647) 0.1806 1.38 30.8 261.7
137 (22699) 0.1795 1.37 27.5 262.9
138 (23174) 0.1833 1.42 55.6 270.3
139 (23186) 0.2110 1.47 52.8 262.1
(23301) see below
140 (23405) 0.120 1.34 63 256
141 (24701) 0.2028 1.47 47.5 270.0
142 (25800) 0.1993 1.38 35.9 259.4
143 (25869) 0.2089 1.49 26.0 281.3
144 (26761) 0.1787 1.36 55.9 253.0
145 (26929) 0.2205 1.44 46.7 259.0
146 (27561) 0.1452 1.35 35.0 263.7
147 (28918) 0.1784 1.38 6.1
148 (29053) 0.0944 1.28 48.9 259.7
149 (29433) 0.1033 1.29 35.5 266.5
150 (29591) 0.1225 1.29 26.6 267.2
151 (29944) 0.1884 1.41 23.7 274.3
152 (29973) 0.1808 1.37 27.9 262.7
153 (30435) 0.2259 1.46 48.5 253.3
154 (30764) 0.1953 1.39 29.5 261.7
155 (31020) 0.1943 1.40 38.3 259.5
156 (31097) 0.1660 1.41 40.9 258.6
157 (31284) 0.1862 1.40 15.8 269.3
158 (31338) 0.1289 1.32 33.2 270.9
159 (31817) 0.1613 1.36 36.3 265.5
160 (32395) 0.2073 1.43 38.7 260.2
161 (32455) 0.2007 1.41 18.2 268.7
(32460) see below
162 (32724) 0.1626 1.38 33.3 267.9
163 (33753) 0.1643 1.33 37.5 264.5
164 (34919) 0.1855 1.45 29.5 264.6
165 (35016) 0.1695 1.36 21.2 270.2
166 (35630) 0.1940 1.41 19.8 268.8
167 (36182) 0.1463 1.34 53.0 256.4
168 (36274) 0.1755 1.41 45.6 273.8
169 (36941) 0.0975 1.27 37.0 262.8
170 (37155) 0.1189 1.33 40.9 270.1
171 (37452) 0.1597 1.35 38.9 266.1
172 (37578) 0.197 1.42 61 247
173 (37590) 0.1933 1.40 37.3 264.1
174 (38046) 0.1807 1.37 29.0 262.5
175 (38292) 0.2074 1.44 56.9 250.2
176 (38470) 0.1456 1.36 42.5 265.5
177 (38553) 0.174 1.40 60 251
178 (38579) 0.1403 1.34 47.4 258.9
179 (38613) 0.136 1.35 12
180 (38684) 0.1877 1.39 23.8 263.1
181 (38701) 0.1909 1.39 26.4 267.6
182 (38709) 0.2491 1.54 29.9 260.5
183 (38830) 0.1747 1.40 47.0 275.2
184 (39266) 0.2475 1.52 1.2
185 (39282) 0.2014 1.41 14.3 268.6
186 (39294) 0.1229 1.32 62.8 267.9
187 (39301) 0.1757 1.39 52.5 253.7
188 (39382) 0.167 1.34 60 250
189 (39405) 0.1976 1.39 26.1 262.3
190 (39415) 0.2058 1.45 56.3 249.8
191 (39427) 0.1749 1.37 34.7 260.9
Objects with a large inclination or osculating eccentricity
192 (15376) 0.2340 1.52 40.8 256.5
193 (19752) 0.1783 1.41 52.8 292.9
194 (23301) 0.1893 1.43 50.8 289.8
195 (32460) 0.2598 1.57 28.2 267.5
Notes to the four last objects:
The present osculating eccentricities of (15376) and (32460) are greater
than or close to 0.30, but there are other objects like (4446) with
similar or greater values of Epm.
In case of (19752) and (23301) the values of Ip are greater than 20 deg,
which is unusual for a Hilda asteroid. Comparatively large values of TL
result for these two asteroids.
In a comparison with Part 1, the last digits of Epm and Ampl of these four
objects show small differences. Due to the simple sun - Jupiter - Saturn model
of the forces, such differences will appear, if the basic osculating elements
refer to different epochs.The near 5/2 commensurability of the mean motions of Jupiter and Saturn gives rise to perturbations with periods of about 900 yr in the orbital elements of these bodies. The angular arguments of these perturbations contain the mean longitudes of the two planets by the difference (5 lms - 2 lmj), with the above designations. If an argument with a period near 900 yr shows up in the variations of a Hilda orbit, another type of resonance in the resonance may be possible. The values of TL are too small, even in comparison with one half of 900 yr. However, there is a chance in the range of the low-eccentricity Hilda orbits in another way:
According to section 4 of Schubart(1991), consider an orbit with a small value of Epm and let a vector represent by its length e' and by its direction lp' (eccentricity and longitude of perihelion, transformed as in Part 1). If periodic effects with periods less than about 100 yr are removed from the data by a filtering process, this vector approximately equals the sum of a vector VE of length Epm rotating in the retrograde way with the rate nu1, and of a shorter vector VA of nearly constant length A with direct rotation according to the rate nu2. The sum of the absolute values of nu1 and nu2 equals ncr introduced in Section 2. If Epm is very small, the absolute value of nu1 is comparatively close to ncr, so that the rotation of VA is slow. Indeed, the natural cases listed in section 2 of Part 1 show comparatively large values of nu2 for Epm near 0.09, but a strong decrease of nu2 with decreasing Epm to small values of nu2 for Epm near 0.025. The decrease of nu2 corresponds to an increase of the period of rotation of VA, and this period can reach values near 900 yr at values of Epm that are slightly smaller than 0.04. Then an argument
α = lpa + 2 lpx -(5 lms - 2 lmj)
will show a very small rate, if lpa equals the polar angle that describes
the direction of VA, and lpx varies with a much smaller rate.
There are no known objects with a nearly vanishing rate of such an α,
but (17397) and (51865) at Epm = 0.04 give values of about 840 yr for the
period of rotation of VA. In these cases long-period variations can arise
from the long period of circulation of α. Actually, such effects have
appeared in an extended integration on the orbit of (51865): The length A
clearly shows long-period oscillations with a period of almost 10000 yr,
but the reason for this was not found at the time of the former study.
According to a recent computation, there are analogous effects with an even
longer period of about 11600 yr in case of (17397).
To demonstrate the connection of these oscillations of A with the slow rotation of an argument α, the following procedure is useful. The vector (e' cos lp', e' sin lp') is studied in rotating coordinates that take away most of the rate nu2, so that the rotation of VA is slow, but the one of VE is fast. Then digital filtering removes all fast frequencies, and the isolated slow rotation of VA appears. Here the rotation of the coordinates proceeds according to the angle (5 lms - 2 lmj - 2 lpx), so that the angle α describes the rotation of the vector VA instead of lpa, and VA only shows a few rotations during an interval of more than 50000 yr. If now lpx represents a linear function of time, that describes the mean revolution of the longitude of perihelion of Saturn, VA describes a nearly circular curve about a center that is displaced by a small amount from the origin of the rotating coordinates to the fixed (-1, 0) direction. This displacement gives rise to the oscillations of A, and the period really equals the period of circulation of α in case of both (17397) and (51865).
The periods of rotation of VA and VE, that correspond to nu2 and nu1 in case of (17397), are equal to 847 and 270.8 yr, respectively, and the center of the approximately circular curve mentioned above is shifted by 0.0035. The period of the relative rotation of VA with respect to VE equals the period of libration of crarg', TL = 205 yr, and A causes the corresponding oscillation of e' about Epm. According to the changes in A, the amplitude of this effect changes between 0.020 and 0.027 with the rotation of α, while the amplitude of libration of crarg' shows a related change from about 50 to 65 deg. Certainly the very long periods of circulation of the perihelia of Jupiter and Saturn have a small influence on these changes as well. The length of VE is almost constant, but nu1 shows small variations that follow the long period of circulation of α.
In case of (51865), the periods of rotation of VA and VE are equal to 835 and 276.5 yr, and TL equals 208 yr. The center of the considered curve is only shifted by 0.0027, and the effects of libration do not change so much with the revolution of α. For instance, the amplitude of libration of crarg' changes between about 43 and 55 deg. To get a fictitious orbit with larger changes of these effects, use the starting values of (51865), here at epoch 2004 July 14, and subtract an amount of about 0.002 from both the values of semi-major axis and eccentricity. Then VA rotates with a period near 875 yr, but VA needs 20 millennia for one rotation with respect to the rotating coordinates introduced above, and this long period rules the comparatively large changes of the effects of libration: Now the amplitude of libration of crarg' changes between 40 and 68 deg. In the rotating coordinates VA produces a more complicated curve that still remains in the vicinity of a mean circle, and the center of this circle is shifted by 0.0067 from the origin to the (-1, 0) direction mentioned before. The fictitious orbit corresponds to Epm = 0.039.
Scanned copies of the following papers are available by the Web pages
of Astronomisches Rechen-Institut Heidelberg. Go to the list of:
Mittlgn. ARI, Ser. B
Schubart J., 1982, Three characteristic parameters of orbits of Hilda-type
asteroids. Astron. Astrophys. 114, 200-204 = Mittlgn. ARI, Ser.B, No. 119
Schubart J., 1991, Additional results on orbits of Hilda-type asteroids.
Astron. Astrophys. 241, 297-302 = Mittlgn. ARI, Ser. B, No. 173
A special paper on details lists further references:
Schubart J., 1994, Orbits of real and fictitious asteroids studied by numerical
integration. Astron. Astrophys. Suppl. Ser. 104, 391-399 = Mttlgn. ARI,
Ser. B, No. 191