Equation of continuity

LangbeinEtAl90 derive the interaction terms to be added to the basic equations of the gaseous model. According to them, the star continuity equation is no longer

$$\frac {\partial \rho_{\star}}{\partial {\rm t}}+ \frac{1}{{\... ... {\partial {\rm r}}({\rm r^2} \rho_{\star} {\rm u_{\star}})=0,$$ (20)

but

$$\frac {\partial \rho_{\star}}{\partial {\rm t}}+ \frac{1}{{\... ...( \frac{\delta \rho_{\star}} {\delta {\rm t}} \bigg)_{\rm lc};$$ (21)

where the right-hand term reflects the time variation of the star's density due to stars interactions (i.e. due to the calculation of the mean rate of gas production by stars collisions) and loss-cone (stars plunging onto the central object).

If $f(v_{\rm rel})$ is the stellar distribution of relative velocities, then the mean rate of gas production by stellar collisions is

$$\bigg( \frac{\delta \rho_{\star}}{\delta {\rm t}} \bigg)_{\r... ...rm c}(v_{\rm rel})}{t_{\rm coll}} f(v_{\rm rel})d^3v_{\rm rel}$$ (22)

In the calculation of equation (14) $f(v_{\rm rel})$ is a Schwarzschild-Boltzmann distribution,

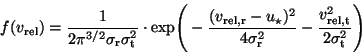$$f(v_{\rm rel})=\frac{1}{2 \pi^{3/2} \sigma_{\rm r} \sigma_{\... ..._{\rm r}^2}-\frac{v_{\rm rel,t}^2} {2 \sigma_{\rm t}^2} \Bigg)$$ (23)

As regards $f_{\rm c}$, it is the relative fraction of mass liberated per stellar collision into the gaseous medium. Under certain assumptions given in the initial work of SS66, we can calculate it as an average over all impact parameters resulting in $r_{\rm min}<2r_{\star}$ and as a function of the relative velocity at infinity of the two colliding stars, $v_{\rm rel}$. LangbeinEtAl90 approximate their result by

$$f_{\rm c}(v_{\rm rel}) = \left\{ \begin{array}{ll} \big(1+q_... ...box{$v_{\rm rel} < \sigma_{\rm coll}$}, \end{array} \right.$$

with $q_{\rm coll}=100$. So, we have that

$$f_{\rm c}(v_{\rm rel}) = \left\{ \begin{array}{ll} 0.01 & \m... ...\mbox{$\sigma_{\rm coll}>v_{\rm rel}$}, \end{array} \right.$$

The first interaction term is

$$\bigg( \frac{\delta \rho_{\star}}{\delta {\rm t}} \bigg)_{\r... ... {\sigma_{\rm coll}}{\sqrt {6}\sigma_{\rm t}} \bigg) \bigg]^2$$ (24)

which, for simplification, we re-call like this

$$\bigg( \frac{\delta \rho_{\star}}{\delta {\rm t}} \bigg)_{\rm coll}\equiv -\rho_{\star} {\rm X_{\rm coll}}.$$ (25)

Since the evolution of the system that we are studying can be regarded as stationary, we introduce for each equation the ``logarithmic variables'' in order to study the evolution at long-term. In the other hand, if the system happens to have quick changes, we should use the ``non-logarithmic'' version of the equations. For this reason we will write at the end of each subsection the equation in terms of the logarithmic variables.

In the case of the equation of continuity, we develop it and divide it by $\rho_{\star}$ because we are looking for the logarithm of the stars density, $\partial \ln \rho_{\star} /\partial t=(1/\rho_{\star})\partial \rho_{\star}/ \partial t$. The result is:

$$\frac{\partial \ln \rho_{\star}}{\partial t} + \frac{\partia... ...( \frac {\delta \rho_{\star}} {\delta {\rm t}} \bigg)_{\rm lc}$$ (26)