

Next: Radial energy equation
Up: The star component
Previous: Equation of continuity
The second equation in Eq.(2.22) has the following
star interaction terms:
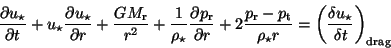 |
(27) |
The interaction term is due to the decelerating force at which stars that move
inside the gas are subject to. As we shall see, an estimate for the force
is given by Eq.(![[*]](./crossref.png) ). Explicitely, it is
). Explicitely, it is
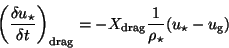 |
(28) |
where we have introduced the following definition:
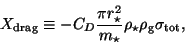 |
(29) |
with
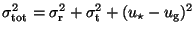 To the end of the calculation of the logarithmic variable version of the equation, we
multiply Eq.(2.33) by
To the end of the calculation of the logarithmic variable version of the equation, we
multiply Eq.(2.33) by
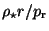 :
:
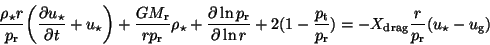 |
(30) |
Pau Amaro-Seoane
2005-02-25
![[*]](./crossref.png) ). Explicitely, it is
). Explicitely, it is