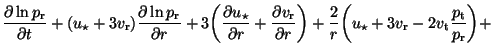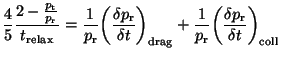

Next: Tangential energy equation
Up: The star component
Previous: Momentum balance
As regards the last but one equation, the interaction terms are:
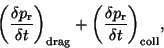 |
(31) |
where
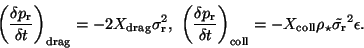 |
(32) |
In order to determine 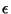 we introduce the ratio
we introduce the ratio 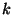 of kinetic
energy of the remaining mass after the encounter over its initial
value (before the encounter);
of kinetic
energy of the remaining mass after the encounter over its initial
value (before the encounter); 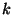 is a measure of the inelasticity of
the collision: for
is a measure of the inelasticity of
the collision: for 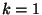 we have the minimal inelasticity, just the
kinetic energy of the liberated mass fraction is dissipated, whereas
if
we have the minimal inelasticity, just the
kinetic energy of the liberated mass fraction is dissipated, whereas
if 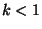 a surplus amount of stellar kinetic energy is dissipated
during the collision (tidal interactions and excitation of stellar
oscillations). If we calculate the energy loss in the stellar system
per unit volume as a function of
a surplus amount of stellar kinetic energy is dissipated
during the collision (tidal interactions and excitation of stellar
oscillations). If we calculate the energy loss in the stellar system
per unit volume as a function of 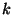 we obtain
we obtain
![\begin{displaymath}
\epsilon=f_{\rm c}^{-1}[1-k(1-f_{\rm c})].
\end{displaymath}](img206.png) |
(33) |
We divide by 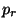 so that we get the logarithmic variable version of the equation.
We make also the following substitution:
so that we get the logarithmic variable version of the equation.
We make also the following substitution:
The resulting equation is
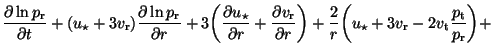 |
|
|
|
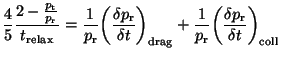 |
|
|
(35) |


Next: Tangential energy equation
Up: The star component
Previous: Momentum balance
Pau Amaro-Seoane
2005-02-25
![]() so that we get the logarithmic variable version of the equation.
We make also the following substitution:
so that we get the logarithmic variable version of the equation.
We make also the following substitution: