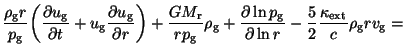

Next: Radiation transfer
Up: The gaseous component
Previous: Equation of continuity
We modify equation number (2.9) of LangbeinEtAl90 in the following way:
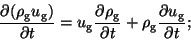 |
(43) |
we substitute this equality in their equation, divide by 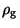 (
(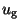 is the variable in our code) and make use of the equation of continuity for the
gas component. Thus, we get the following expression:
is the variable in our code) and make use of the equation of continuity for the
gas component. Thus, we get the following expression:
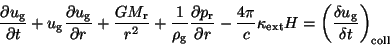 |
(44) |
To get the interaction term we use the mass and momentum conservation:
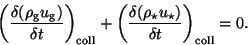 |
(45) |
We know that
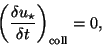 |
(46) |
thus,
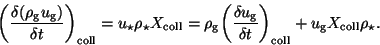 |
(47) |
Therefore, the resulting interaction term is
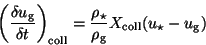 |
(48) |
In the case of the stellar system
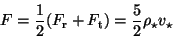 |
(49) |
By analogy, we now introduce 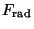 in this way
in this way
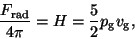 |
(50) |
where 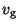 is per gas particle.
is per gas particle.
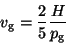 |
(51) |
As means to write the equation in its ``logarithmic variable version'', we multiply
the equation by
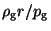 , as we did for the corresponding momentum balance
star equation and replace
, as we did for the corresponding momentum balance
star equation and replace 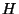 by
by
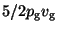 ,
,
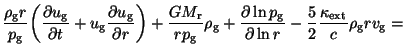 |
|
|
|
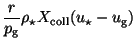 |
|
|
(52) |


Next: Radiation transfer
Up: The gaseous component
Previous: Equation of continuity
Pau Amaro-Seoane
2005-02-25
![]() , as we did for the corresponding momentum balance
star equation and replace
, as we did for the corresponding momentum balance
star equation and replace ![]() by
by
![]() ,
,