We extend here and improve the work done by LangbeinEtAl90 by resorting to a more detailed description of the radiation transfer Castor72.
Consider a radiation field; we place a surface element ![]() with a
surface normal
with a
surface normal ![]() , see Fig.(2.1); the radiation energy which passes
through
, see Fig.(2.1); the radiation energy which passes
through ![]() per unit time at angle
per unit time at angle ![]() to
to ![]() within a
small range of solid angle
within a
small range of solid angle ![]() given by the directional angles
given by the directional angles
![]() and
and ![]() is
is
| (53) |
The radiation intensity
![]() is defined as the amount of energy that
passes through a surface normal to the direction (
is defined as the amount of energy that
passes through a surface normal to the direction (![]() ,
,![]() ) per unit solid angle
(1 steradian) and unit frequency range (1 Hz) in one second. The intensity of the total
radiation is given by integrating over all frequencies,
) per unit solid angle
(1 steradian) and unit frequency range (1 Hz) in one second. The intensity of the total
radiation is given by integrating over all frequencies,
| (54) |
The three radiation moments (the moments of order zero, one and two) are defined by:
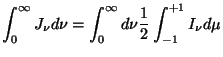 |
|||
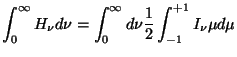 |
(55) | ||
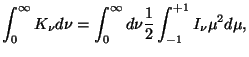 |
| (56) | |||
In the equations
![]() and
and
![]() are the absorption and extinction
coefficients per unit mass
are the absorption and extinction
coefficients per unit mass
| (59) |
![]() is the cooling function,
is the cooling function, ![]() the Planck function and
the Planck function and
![]() the
scattering coefficient per unit mass. We have made use of
the
scattering coefficient per unit mass. We have made use of
![]() ,
,
![]() ,
and the Kirchhoff's law,
,
and the Kirchhoff's law,
![]() (
(![]() is the emission
coefficient), so that the right-hand terms in Castor72 are the corresponding given here.
is the emission
coefficient), so that the right-hand terms in Castor72 are the corresponding given here.
We now look for the logarithmic variable version of both equations;
for this aim, we divide Eq.(2.63) by ![]() and multiply Eq.(2.64) by
and multiply Eq.(2.64) by
![]() ,
,
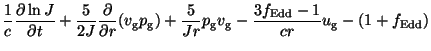 |
|||
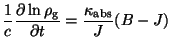 |
(60) |
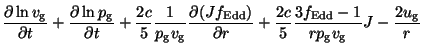 |
|||
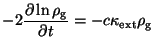 |
(61) |